Summary
A survey carried out on dry-stone walls of the central Andes allowed us to recognize that those walls were erected using a unit of measurement of 1.536 cm, the same that was used in the construction of similar works in Italy and Greece. In both areas the same techniques were applied, but only in South America there are signs of an evolution with clear transitions between them.
Introduction
The close similarities between the megalithic walls - and in particular the polygonal walls - that are found in different parts of the world are not the result of chance but of frequent exchanges between cultures. However there is a strong skepticism by many specialists against the above mentioned hypothesis. They claim that those walls are not very ancient, prehistoric. The polygonal walls of South America are commonly attributed to the Incas, although the Inca domain was very limited in time (1450-1532) in relation to the complexity of the structures in question. Some Italian scholars firmly maintain that polygonal walls are works built by the Romans during their territorial conquests (Polito, 2011).
The perfect seam of the polygonal blocks did not have until recently a satisfactory explanation. Only by means of precise measurements of the space that should be occupied by the blocks they could perfectly fit one another. Examining the polygonal walls of some cities of Lazio, Tuscany and Abruzzo (Mortari, 2012a), it was possible to establish that the megalithic builders adopted for the sides of the polygons a unit of measurement equal to 1.536 cm, quite distinct from the units adopted afterwards by various people of the Mediterranean coasts. Those builders also adopted a sexagesimal division of the right angle, different from the nonagesimal subdivision that has come down to us.
Extending this research to Greece, even if limited to the Milos island and Athens, I obtained similar results (Mortari, 2012b). Therefore those works have preceded not only the Roman and Etruscan civilizations but also the Greek one. Since the indigenous population of Greece, before the arrival of Indo-European-speaking populations, consisted of the Pelasgians, as is evidenced by the most ancient literature, and the highest concentration of cities with walls similar to those we are treating is found in Argolis peninsula, many researchers think that the cities equipped with polygonal walls present on Italian territory were founded by Pelasgians coming from the basin of the Aegean Sea. For this reason it seemed appropriate to call "Pelasgian finger" the unit of measure employed in Italy and Greece (Mortari, 2012b).
In the Mediterranean area four major techniques can be distinguished that were used for the construction of megalithic walls. Proceeding from the least to the most advanced ones they are:
Raw stone walls. The walls of this type derived from the superimposition of stones in their natural state with the purpose of supporting or protecting a ground behind or create a vertical wall of defense. There are some examples at Amelia (Figure 1) and Artena.
Roughcast stone walls. The walls of this class correspond to those described by Mortari (2012b) in Italy and considered megalithic works of second way. The stones are juxtaposed without modifying in an appreciable way the contours and - unlike the first manner - exposing outside a face flat as much as possible, so as to constitute a fairly uniform wall. The traits left empty were filled with smaller stones. Examples, in Italy, include the defensive walls of Roselle (Figure 2) and Norba (Figure 3), and, in Greece, some parts of the walls of Mycenae and Tiryns.
Polygonal stone walls. Sometimes the walls of the classes just considered above are also called polygonal, but this name should be reserved for buildings in which the faces of the elements are made deliberately flat, and the contours are irregular polygons, as we can see for example in Amelia (Figure 4), Alba Fucens (Figure 5), but also in Greece, in Athens, in a modest wall present at the foot of the acropolis (Figure 6). The accuracy achieved in that kind of construction - which does not leave open spaces between the various blocks - is only possible with the use of metal tools. In Figure 7, which shows part of the polygonal wall of Cori, one can see the marks left by a chisel on the limestone rock. The jump in quality between the works of the second type and the polygonal stone works is due to the fact that previously stones were worked with lithic tools, making it possible to get limited touches. In all the polygonal walls of Greece and Italy is evident the straightness of the segments of the contours, the presence of curved edges being generally very sporadic. In Greece, probably shortly before the adoption of the squared stone walls, a kind of shaping of the stones appeared that since the classical period has been called "Lesbian work", where curve contact surfaces were very frequently obtained; we can see an interesting example of this technique in the substructure of the temple of Apollo in Delphi (Caviasca, 2007).
Squared stone walls. From the beginning Greeks and Romans had widely adopted the squared stone technique. This technique has been developed only after the adoption of new tools for working stones, no longer by hammering but by cutting. These tools could be the saw or the wire saw. There is not yet evidence that walls of this kind were built by the Pelasgians. In the Mediterranean, the oldest works of this more advanced way are in Egypt: in Figure 8, taken from Wikipedia, we see part of the funerary complex of the pharaoh Djoser at Saqqara.
Consequently, I went to control whether the polygonal walls that are present in South America were built by measuring the spaces with the same unit of measurement found in Italy and Greece. This looks like a solid argument in order to verify, or falsify, the official way of thinking, according to which the works done with polygonal stones in places as distant and apparently so isolated as the Mediterranean sea and South America are similar just by chance.
Observations
The observations referred in this article were carried out in the area of the plateau of the central Andes, between Cuzco and Tiwanaku. Even here there are roughcast, polygonal and squared stone walls. Original works of the first type are lacking.
A wall of the second type is located in Sillustani (Figure 9). In the background the wall is a roughcast stone work while in the foreground it is a rough stone work. However it is evident that this part is recently rebuilt. Other roughcast stone walls surround the oldest neighborhoods in Ollantaytambo (Figures 10 ÷ 12); here we can see that to have a wall as flat as possible elements were chosen which already had a naturally flat surface, implying possibly to retouch the contours, especially for smaller stones, used to occlude the empty spaces between the greater blocks. In Machu Picchu roughcast stone works are represented by retaining walls of a few meters in height (Figure 13). Here, in the vicinity of the temple of the Sun, it is worth noting a low wall (Figures 14 and 15) that reveals important detail processing. In particular, to the block in the center of Figure 16 has been reserved a privileged support, obtained by properly shaping the two elements below it with two incisions decidedly deeper than it was used in the past; this shaping must have been performed not with lithic instruments, as it had always occurred previously, but by means of new metallic tools. Unlike the Mediterranean region, where, as we have already seen in Figure 7 of Cori, hammer and chisel were used to shape the limestone stones, in the central Andes the tools used are hammer and point because rocks of igneous nature are much more resistant. We can see the marks left by the percussion of a point on some blocks of Sacsayhuaman and Ollantaytambo in Figures 17 and 18.
Even the wall of Figure 19, whose left edge is the most eastern part of the block de las tres portadas of Machu Picchu, shows some elements that have been modeled in order to both allow a better interlocking of the stones and greatly reduce the presence of wedges which fill the spaces between the various elements. Moreover, in the wall section of Figure 20, which belongs to the same block and forms its southern edge, the finishing touches were more pronounced, and typical polygonal contours have already begun to be outlined.
An evolution is also recognizable within the type of the polygonal walls in the strict sense of the word. The simplest forms are found in Pisac (Figure 21) and the Ollantaytambo Fortress (Figure 22): they are characterized by having the sides of the polygons for the most part straight, being curved edges infrequent. It can be noted that often the contour edges are trimmed off, with a consequent ashlar appearance. This is probably due to the fact that during the transport and installation of the blocks it was possible that the edges already processed were accidentally blunted. To make up for the same incident when the edges concerned were those perpendicular to the outer surface, a next step was to shape the element that was to cover the defect with an expansion that fill it (Figure 23) or shaping the corner that would receive the defective stone with an appropriate curvature (Figure 24). If the defect was not manifested the angles were kept normal, and the curvature needed to compensate for much greater volume deficiencies, due to the conformation of the stone already in place (Figures 25 and 26), as is observed for example at the fortress of Ollantaytambo. Finally, in Figures 27 ÷ 29, a further evolutionary step can be observed outside the north side and the south side of the temple of the three windows of Machu Picchu. One can see that the elements are mostly trapezoids tending to become rectangles. It seems that that trend will be a prelude to the introduction of walls with squared stones, as we can see in the background of Figure 28.
Measurements of edges. Measures of edges belonging both to polygonal and squared stones were performed to check which was the unit of measurement adopted. The stones more suitable for this task were the polygonal stones, and this is explained by considering that their perfect joints require that the measures of the spaces to be filled should be determined with great precision. On the contrary, for the squared stones there is a large tolerance, as it is found, for the fact that there is a frequent unevenness in the values of heights. This is the reason why only in a few cases squared stones have shown useful dimensions for our purpose.
At Ollantaytambo the lower sides of two elements with a shape of inverted trapezoid were measured (Figures 30 and 31). The results were of 59.9 and 25.3 cm, that is respectively 39.0 and 16.5 times the Pelasgic finger (pf) of 1.536 cm.
To the upper part of the fortress of Ollantaytambo belong the measures of the sides represented in the Figures 32 ÷ 44; they were of 36,85 38,4 89.9 89.9 89.0 89.0 28.4 35.3 40.7 128.3 56.0 56.8 20.8 cm and correspond respectively to 24.0 25.0 58.5 58.5 57.9 57.9 18.5 23.0 26.5 83.5 36.5 37.0 13.5 pf.
In Cusco, the ancient capital of the Incas, measures have been taken in the wall to which belongs the famous piedra de 12 angules. The wall, built with polygonal stones, delimits a block of about 50 x 40 m and is preserved on three sides. The sequence of Figures 45 ÷ 60 begins in the upper part of the street Hatun Rumiyoc. For each image the two coordinates of the central point of the measured side are provided; they have as a reference the low corner at the left of the photo and are expressed with a sufficient approximation in tenths of width and height. The length of the side in question is then added, expressed both in centimeters and in Pelasgic units: Figure 45 (4 2 87.6 57.0), 46 (7 3 78.0 50.78), 47 (7 2 89.9 58.5), 48 (3 4 57.6 37.5), 49 (6 2 28.0 18.23) (7 7 49.9 32.5) (2 6 69.5 45.25), 50 (7 1 61, 0 39,71), 51 (8 3 68.5 45.0), 52 (3 4 55.3 36.0), 53 (5 4 67.2 43.75), 54 (6 6 66.8 43,5), 55 (7 4 86.4 56.25), 56 (5 3 28.4 18.5), 57 (4 3 97.5 63.5), 58 (5 4 24.9 16.21 ), 59 (7 1 35.59 54.5) and 60 (8 5 82.6 53.78) (5 1 119.0 77.5).
At Sacsayhuaman, the fortress of Cusco, were taken the photos reproduced in Figures 61 ÷ 73. The measurements yielded the following results: 202.0 238.1 63.0 32.3 80.7 98.3 158.2 54.5 71.4 55.3 89.9 79.9 and 59.9 + 63.0 cm, which correspond to 131.5 155.0 41.0 21.0 52.5 64.0 103.0 35.5 46.5 36.0 58.5 52.0 and 39,0 + 41.0 pf. The last two measurements refer to the two sides located at the base of the same stone which is found at the center of the image. At a first glance, overall, the wall does not seem to be a very fine workmanship, but looking at the sixth picture one has a different impression.
Among the most advanced works of the polygonal technique there is the temple of the three windows of Machu Picchu, which opens onto the plaza sagrada. In Figure 27, the bottom side of the stone overhanging the double meter measures 113.2 cm, which is equivalent to 73.7 pf.
In the same square appears the main temple, which is visible in the background of Figure 28. From its back comes the photo of Figure 74; the low side of the block measures 137.6 cm, equivalent to 89.58 pf. On the left side was also measured the block of Figure 75: it measures 131.3 cm (85.5 pf).
Behind the main temple is placed the so-called "sacristy". To its outer wall belongs the block of Figure 76, the base of which is 78.0 cm (50.78 pf). Figures 77 and 78 show two indoor parts: in the first part, the base of the central block measures 62.1 cm (40.4 pf), while the base of the smaller stone below it is 35.3 cm (23.0 pf); in the second one, the lower stone between the two niches has a height of 28.2 cm (18.4 pf), while the two lower rows have heights of 27.6 and 38.8 cm (18.0 and 25.26 pf).
Further south is the temple of the Sun. Only the outer part of the wall to the southwest is measurable; it is so well built that it is called the "perfect wall" (Figure 79). In fact, unlike what usually is found in the walls of this type, at least five of its 10 rows - the intermediate ones - have a constant height. The lower row is fully visible only on a short distance to the right and shows a height of 28.3 cm. The height of the second row varies in a discontinuous manner between a minimum of 34.9 cm to the right and a maximum of 40.7 cm in the middle, with 36.5 cm to the left. The third row varies its height continuously from 46.9 and 36.5 cm. The fourth row is very regular, with a constant height of 23.4 cm (15.23 pf). The fifth row measures 24.9 cm and 25.0 cm from the right to the left (16.21 and 16.27 pf). The height of the sixth row is 21.2 cm on the left and 21.1 cm on the right (13.80 and 13.74 pf). The height of the seventh row is consistently of 20.2 cm (13.15 pf) and the eighth row is of 19.6 cm (12.76 pf). For the ninth row, because of its location, I was able to measure only the part reachable for me, on the left, which is 17.7 cm high (11.52 pf). The measurement of the seventh row, the only found with the nearest to a quarter of a Pelasgic finger, suggests that the rod used for the measurements had the minimum subdivision of a quarter of the unit and that measures approximate to an eighth were made by means of an estimate. On the other hand only a craftsman who knew how to work with great precision, as is the case of who made this "perfect wall", could resort to such an assessment. It is likely that the great precision used for this wall is linked to the size of its elements, which are modest in comparison to the stones of other works.
Not all the works are finished with the precision observed in the perfect wall of Machu Picchu. For example, in Pisac, buildings were erected with this technique (Figure 80), but the height of the squared elements is not taken care of, so that you can find that it is a multiple of the Pelasgian finger. This fact can be observed also in the center of Cusco, where walls of this type are abundant; at a first glance they seem perfect, but then you can notice that the heights of the rows are not uniform. Even in the famous Koricancha the dimensions of the elements do not allow to easily check whether the Pelasgian finger was used here for the measurements.
To find more accurate constructions one must move further south, to Sillustani. The place is known for the presence of various funeral towers, named chullpas, built predominantly with squared stones. In Figure 81 is shown the lower part of an original tower, relatively well preserved, not restored as the next twin tower, visible in Figure 4. The access is very small (Figure 82), and from here, to the right, the heights were measured of the14 stones that form the second row. The upper thread is very regular and continuous. Only at the middle of the element n. 8, at the opposite side from the entrance, there is an evident step (Figure 83); this suggests that the row was started from above the entrance and was extended simultaneously by the two sides. The bottom row is less regular, probably because its stones have had to adapt to a foundation soil that was not perfect: Figure 84 shows one step, placed between the 4th and the 5th element. In the same figure one can observe a particular that indicates the accuracy with which the stones were processed in the quarry: on the two central blocks and on the ones located in the higher part some "flames" are visible which are orange in color and continuous between the four blocks. At the bottom on the left one can see the signs of the percussion of a point.
Here I report the measurements (in centimeters) of the heights of the left and right edges of each of the 14 elements and, in parentheses, the corresponding values expressed in Pelasgian fingers. The sign / indicates lack of measure due to the excessive variability of the height. 1: 67.6 (44.0) - 67.6 (44.0); 2: 89.1 (58.0) - 88.4 (57.55); 3: 88.4 (57.55) - 87.5 (57.0); 4: 87.5 (57.0) - /; 5: 92.1 (60.0) - 92.2 (60.0); 6: 92.1 (60.0) - 92.2 (60.0); 7: 92.2 (60.0) - 88.3 (57.5); 8: 88.3 (57.5) - 85.3 (55.5); 9: 84.9 (55.27) - /; 10: / - 89.8 (58.5); 11 90.6 (59.0) - 94.1 (61.26); 12 : 94.1 (61.26) - 95.2 (62.0); 13: 95.2 (62.0) - 93.7 (61.0); 14: 93.7 (61.0) - 93.3 (60.74). It can be noted that 15 out of 25 values are integer multiples of the Pelasgic unit and that 4 measurements were made using ¼ of the same unit.
In Tiwanaku, Bolivia, we can see that the cutting technique is more sophisticated and - we may say - more evolved. We can be surprised by the smoothness of the surfaces which reflect the sunlight like a mirror as in Figure 85 or by the perfection both of the longitudinal groove of Figures 86 and 87 and of the holes 4.6 mm large and 10 mm deep distributed every 35 ÷ 36 mm along the groove. We find evidence that the Pelasgic finger is still the unit of measure adopted. In Figure 88 the remains are shown of one of the doors that are dispersed on this site and in a few cases could be obtained from a single lithic block. The bands of different width measure 15.8 14.2 ÷ 14.3 12.6 ÷ 12.7 11.7 cm. The width of the same bands - with the exception of the first - become, after the double angle, 14.2 ÷14.3 12.7 25.0 cm. These values correspond to 9.24 ÷ 9.31 8.20 ÷ 8.27 7.62 10.29 16.28 pf. Even in this case, as in Machu Picchu, we can notice that there are frequent measures approximated to ¼ pf.
Figure 89 shows the lintel of another door. It was saved by the foolishness of entrepreneurs who built the railroad La Paz-Guaqui just through the archaeological site of Tiwanaku and raged on the stones of larger size to reduce them into fragments with the help of dynamite and arranged them as ballast under the sleepers of the tracks. It was saved because, when they made two holes of 50 mm in diameter to insert the explosives, the vibrations of the perforations, fortunately, broke the rock into three pieces (Figure 90), making it impossible to apply the charges. The longitudinal bands of the architrave have widths of 26.0 15.4 ÷ 15.5 14.2 ÷ 14.4 12.9 ÷ 13.0 11.5 and 9.6 cm, corresponding to 16.9 10.0 ÷ 10.1 9.24 ÷ 9.37 8.4 ÷ 8.5 7.5 and 6.25 pf. Also here, therefore, we note that the measurements were made approximating them to ¼ of their units of measure.
The archaeological site of Tiwanaku was incomparably richer than today, as we can infer from the descriptions made by some Spanish writers such as Pedro Cieza de Leon, who was the first to visit the site in 1549; in 1553, in his Chronicle of Peru, he described Tiwanaku as a city not very wide but with memorable stone buildings, surrounded by cyclopean walls. In one of these buildings, "there is a room 14 m long, 7 m wide, with large doors and lots of windows". Another writer, Jimenes de la Espada, described "a palace which is the eighth wonder of the world, with stones 11 meters long and 5 m wide processed to get stuck into each other without seeing the connection".
We can get an idea of these joints observing the precision with which the surfaces were obtained in Figure 91. Indeed, everything suggests that the buildings were assembled with perfect joints. Some more determinant modules were kept tied with cramps of bronze, of which in the greater part of the cases remained only the groove (Figure 92).
Measurements of angles. In the polygonal stone works a few angles were measured where - with a criterion similar to that used for the measurements of the edges - it seemed obvious that they were shaped to receive a new element of the wall. The aim was to compare their measurements with those carried out on the Pelasgian walls of Italy and Greece, remembering that those measures revealed a sexagesimal subdivision of the right angle.
The determination of the amplitude of the angles found some difficulties, due to the fact that sides are often constituted not by a single rectilinear segment but by two or three segments, thus giving a false impression that the sides are curved instead of broken lines. The angle values were determined on photographs taken by placing the lens in front of the vertex of interest in order to minimize the parallax error.
From the fortress of Ollantaytambo come the images of Figures 93 and 94, from which I derived the angular values of 97 and 93 °. To Sachsywaman refer Figures 95 and 96, with angles, respectively, of 95 and 107 °. Belong to Cusco finally the stones of Figures 97 ÷ 101; the angles obtained resulted, in succession, of 92 91.5 91 92 and 85.5 °. Since in South America the side lengths are multiple of the same unit of measurement of 1.536 cm found in the Mediterranean area, we might have inferred an analogous coincidence for the angle values, with the use of the same unit of 1.5 °. On the contrary the values determined in the central Andes seem to be multiples of 1 °. In order to dispel the doubt that this could be due to errors made in the measurement operations, which are approximated to 0.5 °, it can be useful to analyze in more detail the Figure 101. The angle in question belongs to the stone in the center of the photograph and precisely is found in the lower right part; each of the sides concerned is formed by two sections with slightly different direction. If we measure the angle formed by the two parts nearest to the vertex, we obtain 85.5 °. If we use the most distant traits, the opening is 84.5 °. Finally, if we use one stretch next to the corner and the other far from it, we have in both cases 85 °. It is inferred that each of the sides of the two differently oriented sections are deviated from each other by 0.5 ° (i.e. the difference between 84.5 and 85 °), which can be considered as the half of the unit that was being used.
The doors. This argument gives us the opportunity to try to test the value of the unit used to measure angles. The door jambs related to the walls we are studying are in fact not vertical but trapezoid-shaped, like that of Ollantaytambo in Figure 102. The form may have been dictated by the previous way of building. In the oldest walls we do not find traces of door jambs because surely they were entirely of wood, given the great difficulty of mould stones before the invention of the bronze.
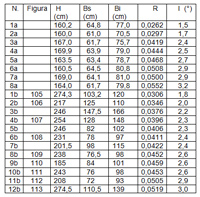
We can infer that the jambs were inclined because the need to counteract the lateral thrust of the stones which were on the sides of the door, since the elements were made of just roughcast stones and therefore to some extent pushing, as can be inferred by looking at the photo of the Figure 103, taken at Ollantaytambo. Doors with similar form can be found in Cerveteri (Figure 104). The inclination of the sides of these doors in the shape of a trapezium was determined by measuring the height and the two bases. In the first part of the Table 1 we have the data of some of the doors of the “cube” tombs belonging to the necropolis of the Banditaccia near Cerveteri (sixth century BC). In the second part there are the data of the doors measured in Peru. These data are listed for increasing inclination of the sides. In the various columns are: the height H, the smaller base Bs and the greater one Bi, the ratio R between the half-difference between the bases and the height and finally the tilt I.
As for the South American region, most of the doors of the table are represented in Figures 105 ÷ 113, the number of figures appearing in the second column. The door of the figure 105 belongs to the block of Cusco surrounded by the polygonal wall and is the best preserved. In the second half of the table, the numbers 2, 7 and 12 refer to Pisac, the numbers 3, 5, 6, 8, 9 and 10 to Ollantaytambo, the numbers 4 and 11 to Machu Picchu.
To complete the series of doors observed we cannot pass over in silence the door of the fortress of Sachsyhuaman, about 2.9 m high with an inclination of the jambs of about 3 °, determined from the photo shown in Figure 114.
From the comparison of the data in the table it seems confirmed that in South America were used grades as we use them today. Even if the test is not exhaustive (the data in the table are very scanty), it seems that in that region the inclination of the jambs of the doors tended to be around the values of 2.0 2.5 and 3.0 °, with a preference for the value of 2.5 °.
With regard to the data of Cerveteri, it seems that even here there is some concentration around the value of 2.5 °, which would suggest that the Etruscans had also adopted the degree found in the Andes. I tried to allay the legitimate concerns by measuring the angles of a polygonal wall belonging to one of the oldest tombs, of the seventh century BC, in the same necropolis of the Banditaccia in which I measured the sizes of the doors. The conditions are not very suitable for such an operation because the stones, consisting of the local "red tuff with black scoriae", do not have well preserved edges. However, the measurement of the angle of 91 ° obtained from the photo shown in Figure 115 suggests that with some probability as early as in the seventh century BC in our country the system for measuring the angles was already adopted that is in use today.
Conclusions
In the central Andes and the Mediterranean area a common succession of megalithic construction techniques was found. A first technique makes use of lithic tools in order to mould the stones with a very little removal of rock volumes. With the second technique a great removal of volumes becomes possible because of the introduction of bronze tools; polygonal stone walls were therefore built. With the third technique stones take a parallelepiped shape; they are no longer shaped by hammering but are cut with a saw or a wire saw.
Crucial to establish that a common succession is not a pure coincidence it was to have determined that the processing of polygonal and squared stones was ruled by the execution of measures that made use of the same unit of 1.536 cm.
Moving on to examine the differences, it was noted with surprise, although we would need a confirmation, that, for the measurement of angles, in the Andean region a nonagesimal subdivision of the right angle was adopted while, on the contrary, in the Mediterranean area a sexagesimal subdivision was in use.
With regard to the differences between the two areas, only in South America it is possible to observe an evolution between the various types of walls. Namely the polygonal stone works show not only a clear derivation from those works made with just roughcast stones but also a transition to the works carried out by the technique of squared stones. Such evolution was not observed in the Mediterranean area, despite to the fact that the stones used in this region, mostly of limestone, were more favorable to the testing of new processing methods.
In conclusion we can say that in the central Andes, and specifically in Peru, three revolutionary inventions have occurred. The first invention consisted of the bronze metallurgy, testified by the more evolved roughcast stone walls of Machu Picchu, which present a more incisive shaping of the stones; this result was possible only with the use of a hammer and a metal point.
The second invention was that of linear measurements. The possession of a rigid metal such as the bronze allowed to design a sample rod with a number of engravings at equal distances and to reproduce some copies of it so that various operators could use them in the same time in different places in order to take standard measurements. It is a great innovation because until that moment measures in a precise sense were reserved to the dimension of the time. Until that moment small lengths were carried by means of a provisional rod while longer lengths were expressed only in days or fractions of a day away. With regard to the amplitude of the angles, most probably for the first time their determination was done with a great precision.
The third revolution was the invention of tools for cutting stones; the instruments could be wire saws and/or wire saws. In this way it was possible to reduce very much the scrap in the quarry and obtain large blocks more easily.
Works cited
Caviasca M. (2007). L’evoluzione delle tipologie e la natura costruttiva. docenti.polimi.it/caviasca/caviasca/lez4.pdf.
Mortari R. (2012a). 2012 – From the Mayan prophecy to the science previsions. www.prevederecatastrofi.it , 85 pp.
Mortari R. (2012b). Confronto tra mura poligonali d’Italia e Grecia. www.terradegliuomini.com.
E. Polito (2011) edited by. Guida alle mura poligonali della provincia di Frosinone. Province of Frosinone. 96 pp.